³æ¤¸¤¡BªÅ¶¡Âoªi
1. ªÅ¶¡°j±Û¿n(Spatial Convolution)
¤@±i¼v¹³¥i¥H¦bÀW²v°ì(frequency
domain)©ÎªÅ¶¡°ì(spatial domain)¶i¦æÂoªi¡C¥»³¹±N¤¶²Ð¦UºØ¥Î¦bªÅ¶¡°ì²vªiªº¹Bºâ¤l¡A¥]¬A¥iÂo°£°ªÀWÂø°Tªº§¡ÈÂoªi¾¹¡B¤¤ÈÂoªi¾¹¡B°ª´µÂoªi¾¹¡A¥H¤Î¥Î¨Ó¼W±jÃä½t¯S¼xªº¯Á¨©º¸Âoªi¾¹¡B©Ô´¶©Ô´µÂoªi¾¹¡C
ªÅ¶¡Âoªi¾¹(spatial
filter)h(i,j)¤SºÙ¬°Mask/Kenel/Window¡A¼v¹³f(x,y)¸g¹LªÅ¶¡Âoªi¾¹ªº¹Bºâ¡A±o¨ìÂoªi«áªº¼v¹³g(x,y)¡A
![]()
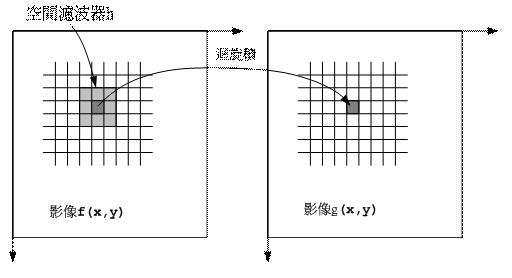
¦¹¤@¹Bºâ¬°°j±Û¿n(convolution)¡A°j±Û¿nªº¹Bºâ¼Ò¦¡¬°"shift-multiply-summation" , shift«ü¥Ñ¥ª¨ì¥k¡B¥Ñ¤W¨ì¤U²¾°ÊÂoªi¾¹h¡A°w¹ï¨C¤@¦¸Âoªi¾¹µøµ¡©Ò²[»\ªºì©l¼v¹³ªº°Ï°ì¶i¦æ¬Û¼¡A³Ì«á²Ö¥[©Ò¦³¼¿n¡A±o¨ìÂoªi¼v¹³g¤W¤@Ó¹³¯ÀªºÈ¡C°²³]ªÅ¶¡Âoªi¾¹ªº¤j¤p¬OM¡Ñ M¡A«h§ÚÌ¥i¥H¼g¦¨:
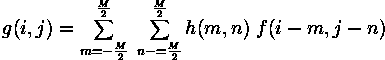
¥Ü·N¹Ï¦p¤U¡G
void
convolution(uc2D &ima1, f2D &h, uc2D &ima2)
{
int i,j,ii,jj;
int N=h.nr/2;
int mac;
for(i=N;i<ima1.nr-N;i++)for(j=N;j<ima1.nc-N;j++)
{
mac
= 0;
for(ii=-N;ii<=N;ii++)for(jj=-N;jj<=N;jj++)
{
mac
= mac + ima1.m[i+ii][j+jj]*h.m[ii+N][jj+N];
}
ima2.m[i][j]=mac;
}
}
2. ¥Î©ó¥·Æ¤Æ¼v¹³ªº½u©ÊÂoªi¾¹
A. §¡ÈÂoªi¾¹(mean filter)
¤@Ó3x3§¡ÈÂoªi¾¹¬O³Ì²³æªº¥·Æ¤ÆÂoªi¾¹(smoothing filter)¡A¨ä«¬ºA¦p¤U

©Î

B.ªx¥Î«¬ÅvÈ¥·ÆÂoªi¾¹(generalized weighted smoothing filter)
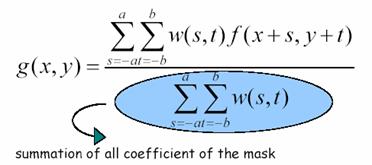
¤@Ó3x3ÅvÈ¥·ÆÂoªi¾¹¨Ò¤l

/*-------------------------------------------------------------*/
//
Convolution of image with mean filter
//
//
³¯¼yÃv¡A2004.10.12
/*-------------------------------------------------------------*/
#include <fstream.h>
#include <math.h>
#include "array.h"
void mean_filter_design(f2D &h, int winsize);
void convolution(uc2D &ima1, f2D &h, uc2D &ima2);
void main()
{
ifstream
in("120x120.raw",ios::binary);
ofstream
out("bin.raw",ios::binary);
uc2D ima1,ima2;
ima1.Initialize(120,120);
ima2.Initialize(120,120);
char c;
for(int i=0;i<ima2.nr;i++)for(int j=0;j<ima2.nc;j++)
{
in.get(c);ima1.m[i][j]=ima2.m[i][j]=c;
}
f2D h;
//filter
mean_filter_design(h, 3);
convolution(ima1, h, ima2);
for(int i=0;i<ima2.nr;i++)for(int
j=0;j<ima2.nc;j++)
out<<ima2.m[i][j];
}
void mean_filter_design(f2D &h, int winsize)
{
h.Initialize(3,3); // Size initialize by 3X3
for(int i=0;i<h.nr;i++)for(int j=0;j<h.nc;j++)
h.m[i][j]=1.0/9.0;
// mean filter's coefficients
}
void convolution(uc2D &ima1, f2D &h, uc2D &ima2)
{
int i,j,ii,jj;
int N=h.nr/2;
int mac;
for(i=N;i<ima1.nr-N;i++)for(j=N;j<ima1.nc-N;j++)
{
mac
= 0;
for(ii=-N;ii<=N;ii++)for(jj=-N;jj<=N;jj++)
{
mac
= mac + ima1.m[i+ii][j+jj]*h.m[ii+N][jj+N];
}
ima2.m[i][j]=mac;
}
}
C. °ª´µ¥·ÆÂoªi¾¹(Gaussian
smoothing filter)
¦b¤@Ó¤GºûªÅ¶¡¡A°ª´µ¤À¥¬ªº¨ç¼Æ©w¸q¬°¡GThe Gaussian distribution in 1-D has
the form:
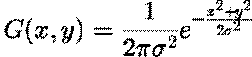
°²³]°ª´µ¤À¥¬ªº¥§¡È¬°0¡A¦Ó£m¬O°ª´µ¤À¥¬ªº¼Ð·Ç®t¡A¦pªG£m=1¡A§ÚÌ¥i¥H±o¨ì¥H¤U¤À¥¬«¬ºA¹Ï¡G
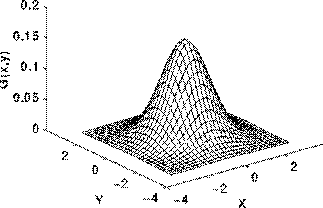
Â÷´²«¬ºAªº°ª´µÂoªi¾¹¨Ï¥Î¾ã¼Æ¨Ó¹Gªñ°ª´µ¨ç¼Æ¡A¨Ò¦p¹ï©ó¤@Ó5x5ªº°ª´µÂoªi¾¹(£m=1)¡A§ÚÌ¥i¥H±o¨ì¥H¤UªºÂoªi¾¹«Y¼Æ¡G

°ª´µÂoªi¾¹¬O¤@Ó¥·Æ¤ÆÂoªi¾¹¡A¥·Æ¤Æµ{«×¬O¥Ñ¼Ð·Ç®t£m¨Ó±±¨î¡A£mȶV¤j¡A¥·Æµ{«×¶V°ª¡A¬Û¹ïªº¡A¼v¹³¶V¼Ò½k¡C
§@·~1¡B
³]p¤@ÓGaussian_filter(
)¨ç¦¡¡A´ú¸Õ3Ó¤£¦Pªº£mÈ(£m=1, £m=2©M£m=5)©M¨âºØ¤£¦PªºÂoªi¾¹¤j¤p(filtersize=5©Mfiltersize=11)¦@¤»ºØ²Õ¦X¡A¥Hmantis500x500.raw¼v¹³¬°¹ï¶H¡AÆ[¹î¤£¦PÂoªi®ÄªG¡C
3. ¥Î©ó¥·Æ¤Æ¼v¹³ªº«D½u©ÊÂoªi¾¹
«Ø¥ß¦bÂoªi¾¹½d³ò¤ºªº¹³¯Àªº²Îp±Æ§Ç(ranking)¨Ó¨M©wÂoªi¿é¥X¡A¦Ó«D¨Ï¥Î°j±Û¿n¡G
¤¤ÈÂoªi¾¹(median filter)¡Gh = median{gk | k=1,2,¡K, M¡Ñ M}
³Ì¤jÈÂoªi¾¹(max filter)¡Gh = max{gk | k=1,2,¡K, M¡Ñ M}
³Ì¤pÈÂoªi¾¹(min filter)¡Gh = min{gk | k=1,2,¡K, M¡Ñ M}
A. ¤¤ÈÂoªi¾¹
¤¤ÈÂoªi¾¹ÂǥѨC¤@Ópixel¾Fªñpixel¦Ç¶¥È±Æ§Çªº¤¤¶¡È¨Ó¨ú¥N¸Ópixelªº¦Ç¶¥È¡C¤¤Èªºpºâ¬O¥ý±N¾Fªñpixel(Âoªi¾¹µøµ¡½d³ò)¦Ç¶¥È±Æ§Ç¡A¦b¨ú¥X±Æ§Ç©~¤¤ªºÈ§@¬°Âoªi¾¹¤¤¶¡¦ì¸m¼v¹³ªº¹³¯ÀÈ¡C¨Ò¦p

¥H¤U¬O¨Ï¥Îbubble sortì²zªº¤¤ÈÂoªi¾¹ªº°Ñ¦Òµ{¦¡¡G
//-----------------------------------------------------
// Median filtering
// 2004.10.18 by
CHEN Ching-Han
//-----------------------------------------------------
void Median(uc2D &InIm, uc2D &OutIm, int WinSize)
{
int r,c, y,x, i,j, n, Area;
unsigned char Buf;
unsigned char *Lst;
n = (WinSize-1)
>> 1;
Area = (2*n+1) *
(2*n+1);
Lst = new char[Area];
Int nr=InIm.nr, nc=InIm.nc;
for (r=0; r<nr; r++)for (c=0; c<nc;
c++)OutIm[r][c] = 0;
for (r=n; r<nr-n; r++)
{
for (c=n; c<nc-n; c++)
{
i=0;
for (y=-n;
y<=n; y++)for (x=-n; x<=n; x++)
{
Lst [i]
= InIm [r+y] [c+x];i++;}
/*---------- bubble sort -------------------*/
for (i=0; i<Area-1; i++)for (j=Area-1; i<j; j--)
if (Lst[j-1] > Lst[j])
{
Buf
= Lst[j-1];
Lst[j-1] = Lst[j];
Lst[j] = Buf;
}
OutIm [r][c] = Lst [Area/2];
// get madian value
}
}
}
§@·~2¡G
½Ð¤À§O¥H7x7ªºmedian, max, minÂoªi¾¹¹ïmantis500x500.raw¼v¹³§@ªÅ¶¡Âoªi¡A©w©Ê¤ñ¸û¤TªÌªº®t²§¡C
B. °Ñ¼Æ¥i½Õªº¤¤ÈÂoªi¾¹¢w¥[Åv¤¤ÈÂoªi¾¹(Weighted median filter)

§@·~3¡G
½Ð°Ñ¦Òmedian¨ç¦¡¡A³]p¤@ÓWeightedMedian¨ç¦¡,¨Ã¥H3X3Âoªi¾¹¤j¤p¬°¨Ò¡A°õ¦æ¥[Åv¤¤ÈÂoªi¡C¨Ï¥Î¤£¦PªºW¨ÓÆ[¬d¥[Åv¤¤ÈÂoªi¹ïfinger300x300Âoªi®ÄªG¡C©Î°²³]W= ¡C
¡C
¶i¶¥§@·~3(option)¡G¨Ï¥ÎÀH¾÷³Ì¨Î¤Æ©Îºt¤Æ³Ì¨Î¤Æ¤èªk§ä¥X¤@²ÕW«Y¼Æ(¾ã¼Æ)¡A¨Ï±o¥[Åv¤¤ÈÂoªi¾¹¥i¥H°õ¦æEdge enhancementªº§C³qÂoªi¡C
4. Ãä½t°»´úÂoªi¾¹(edge
detection filter)

A.
SobelÂoªi¾¹
SobelÂoªi¾¹¨Ï¥ÎªÅ¶¡¤@¶¥¾É¼Æ¨Ó¼W±j°ªÀWªºªÅ¶¡°T¸¹¡A¦b¼v¹³¤¤¡A³o¨Ç°ªÀW°T¸¹³q±`¥Nªí¸û¾U§Qªºª«ÅéÃä½t©Î½u±ø¯S¼x¡C
¤@ºûªº¤@¶¥¾É¼Æ¡G
![]()
¤Gºûªº¤@¶¥¾É¼Æ¥H±è«×(gradient)ªí¥Ü¡G
![]() = Gx + Gy
= Gx + Gy
Gx©MGy¤À§Oªí¥Üx©My¤è¦Vªº±è«×¤À¶q¡A¨äÂ÷´²Âoªi¾¹§Î¦¡¥i¥Hªí¥Ü¦p¤U¡G

±è«×ªº¤j¤p(amplitude)¬O
![]()
©Î
![]()
¦Ü©ó¤è¦V(orientation)«h¬°
![]()
§@·~4¡G
³]p¤@ÓsobelÂoªi¾¹¨ç¦¡¡A¿é¤J11x11ªº¾ã¼Æȸê®ÆÀÉ¡A¿é¥Xamplitude¸ê®Æªí©M orientation¸ê®Æªí¡A¦p¤U¹Ï¡C¥t¥~(option)ø¥Xorientation¤è¦V¹Ï(4Ó¤è¦V§Y¥i)¡C

§@·~5¡G
Ãþ¦üsobelÂoªi¾¹ªº¤@¶¥¾É¼ÆÂoªi¾¹ÁÙ¦³Prewitt, Frei-Chen, Sharrµ¥¡A¨äÂoªi¾¹¤À§O¦p¤U¡G

½Ð³]p³o4ÓÂoªi¾¹(¥]§tSobel)ªºµ{¦¡¡A¨Ã¥Î¦P¤@±i¼v¹³¤ñ¸û4ÓÂoªi¾¹ªº°õ¦æµ²ªG¡C
§@·~6¡G
¦³¨âºØ³QºÙ¬°Ã¹½LÂoªi¾¹(compass filter)ªº¤@¶¥¾É¼ÆÂoªi¾¹¡A´N¬O¤U¹ÏªºRobinsonÂoªi¾¹©MKirschÂoªi¾¹¡A¥¦Ì³£¨Ï¥Î¤@ÓÂoªi¾¹µøµ¡±ÛÂà8Ó¨¤«×±o¨ì8²ÕÂoªi¾¹«Y¼Æ¡A³o8ÓÂoªi¾¹µøµ¡¤À§O©M¼v¹³§@°j±Û¿n¡A8Ó°j±Û¿n·í¤¤ªº³Ì¤jÈ©w¸q¬°edgeªº±j«×(amplitude)¡Aedgeªº¤è¦V(orientation)«h¬O¹ïÀ³ªºÂoªi¾¹µøµ¡¨¤«×½s¸¹(0~7)¡A¨¤«×0(§Yr0©Îk0)¥Nªí««ª½edge¡A¨¤«×3¥Nªí¤ô¥edge¡C
|
|
RobinsonÂoªi¾¹ |
|
|
KirschÂoªi¾¹ |
½Ð³]p³o2ÓÂoªi¾¹ªºµ{¦¡¡A¿é¤J¤@±i¼v¹³¡A¿é¥Xamplitude¼v¹³©Morientation¼v¹³(¨Ï¥Î¨¤«×½s¸¹0~7¡A¥H¹Ï§Î©Î¸ê®Æªí§e²{§¡¥i)¡C
B.LaplacianÂoªi¾¹
©Ô´¶©Ô´µÂoªi¾¹¬O¤@ºØªÅ¶¡¤G¶¥¾É¼Æªº¹Bºâ¤l¡A¥¦¹ï©ó¼v¹³¤¤§Ö³tÅܤƪº°Ï°ì(¥]§tedge)¨ã¦³«Ü¤jªº±j¤Æ§@¥Î¡A¦]¦¹±`µ²¦XZero Crossing Detection(¦p¤U¹Ï)§@¬°Ãä½t°»´úªº¤u¨ã¡C

![]()
![]() ªÅ¶¡(¤Gºû)ªº¤G¶¥¾É¼Æ¡G
ªÅ¶¡(¤Gºû)ªº¤G¶¥¾É¼Æ¡G
LaplacianÂoªi¾¹ L(x,y) ©w¸q¬°:
![]()
¹GªñªºÂ÷´²LaplacianÂoªi¾¹¦³¥H¤U¤TºØ«¬ºA¡G
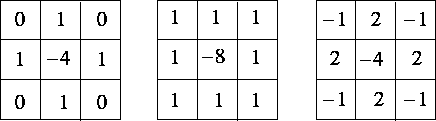
LaplacianÂoªi¾¹ªº¨Ï¥Î¤]±Ä¼Ð·Çªº°j±Û¿n¤èªk¡C¥Ñ©ó¥¦¹ï°ªÀW°T¸¹ªº°ª«×±Ó·P¡A¦P®É¤]·|±j¤Æ°ªÀWÂø°T¡A©Ò¥HÀ³¥Î©Ô´¶©Ô´µÂoªi¾¹«e±`¥ý¶i¦æ¥·Æ¤ÆÂoªi(¦p°ª´µ¥·ÆÂoªi)¡A¥H«K°§CÂø°T¤zÂZ¡C¦ý°ª´µ¥·ÆÂoªi+LaplacianÂoªi»ÝnÂù«°j±Û¿n¹Bºâ¡A¤Q¤À¯Ó¶Opºâ¸ê·½¡A¦]¦¹¦h¼Æ±Ä¥ÎLoG (Laplacian of Gaussian)Âoªi¾¹¡C
LoG
(Laplacian of Gaussian)Âoªi¾¹(zero mean¤Î¼Ð·Ç®t£m) :
![]()
¨ä¨ç¼Æ¦±±¹Ï¦p¤U¡G

¤@Ó9x9Â÷´²Âoªi¾¹«Y¼Æ¨Ò¤l¦p¤U( ¼Ð·Ç®t£m= 1.4)¡G

LoGª`·N¨Æ¶µ
The
LoG operator calculates the second spatial derivative of an image. This means
that in areas where the image has a constant intensity (i.e. where the
intensity gradient is zero), the LoG response will be zero. In the vicinity of
a change in intensity, however, the LoG response will be positive on the darker
side, and negative on the lighter side. This means that at a reasonably sharp
edge between two regions of uniform but different intensities, the LoG response
will be:
- zero at a long distance from the
edge,
- positive just to one side of the
edge,
- negative just to the other side of
the edge,
- zero at some point in between, on
the edge itself.
§@·~7¡G
³]p¤@Ó9x9 LoG (Laplacian of Gaussian)Âoªi¾¹¨ç¦¡¡A¹ïant(gray)600x400¼v¹³¶i¦æedge¼W±jÂoªi¡A(a)¿é¥XLoGÂoªi«á¼v¹³(½Ðª`·NȰ쪺normalization)¡F(b)(option)¿é¥Xzero-crossing¼v¹³¡A¤]´N¬O§ä¥XLoGÂoªi«á¼v¹³ªºzero-crossingªºpixel¦ì¸m¼Ð¥Ü¬°0¡A¨ä¥L¼Ð¥Ü¬°255¡C
5. UnShapeÂoªi¾¹

§@·~8(option)¡G
³]p¤@ÓUnShapÂoªi¾¹¨ç¦¡¡A¨ä¤¤ªºHistogram Shrink¼Ò²Õ¡A´£¨Ñ¤@Ó¥i½Õ±±ªº¾÷¨î¡A¨Ò¦pShrink½d³ò³]©w¦b[0,50]©M[0,150]±N²£¥Í¤£¦Pªºedge±j¤Æ®ÄªG¡C

