The networks that are used to perform associative recall are specific examples of a wider class of physical systems which may be thought of as doing the same thing. This allows the net operation to be viewed as a the dynamics of a physical system and its behaviour to be described in terms of the network's `energy'. Consider a bowl in which a ball bearing is allowed to roll freely
bowl and ball bearing in 3D

This is more easily drawn using a 2D cross section
2d X-section of bowl
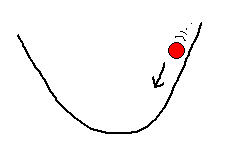
Suppose we let the ball go from a point somewhere up the side of the bowl with, possibly, a push to one side as well. The ball will roll back and forth and around the bowl until it comes to rest at the bottom.
The physical description of what has happened may be couched in terms of the energy of the system. The ball initially has some potential energy. That is work was done to push it up the side of the bowl to get it there and it now has the potential to gain speed and acquire energy. When the ball is released, the potential energy is released and the ball rolls around the bowl (it gains kinetic energy). Eventually the ball comes to rest where its energy (potential and kinetic) is zero. (The kinetic energy gets converted to heat via friction with the bowl and the air). The main point is that the ball comes to rest in the same place every time and this place is determined by the energy minimum of the system (ball + bowl). The resting state is said to be stable because the system remains there after it has been reached
There is another way of thinking of this process which ties in with
our ideas about memory. We suppose that the ball comes to rest in the
same place each time because it `remembers' where the bottom of the
bowl is. We may push the analogy further by giving the ball a
coordinate description. Thus, its position or state at any time
is given by the three coordinates or the position
vector x. The location of the bottom of the bowl,
represents the pattern which is stored. By writing the ball's vector
as the sum of
and a displacement
thus,
, we may think of the ball's
initial position as representing the partial knowledge or cue for
recall, since it approximates to the memory
.
If we now use a corrugated surface instead of a single depression (the bowl) we may store many `memories'.
X-section through corrugated surface
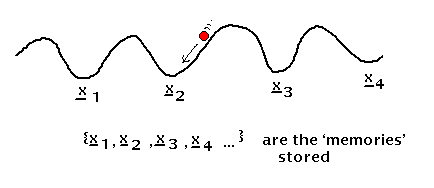
If now the ball is started somewhere on this surface, it will eventually come to rest at the local depression which is closest to its initial starting point. That is it evokes the stored pattern which is closest to its initial partial pattern or cue. Once again, this is an energy minimum for the system.
There are therefore two complementary ways of looking at what is happening. One is to say that the system falls into an energy minimum; the other is that it stores a set of patterns and recalls that which is closest to its initial state. If we are to build a network which behaves like this we must include the following key elements