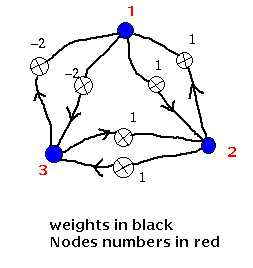
Consider the network consisting of three TLU nodes shown below
3 node Hopfield net

Every node is connected to every other node (but not to itself)
and the connection strengths or weights are symmetric in that the
weight from node i to node j is the same as that from node
j to node i. That is, , and
for all
.
![]() Notice that the flow of
information in this net is not in a single direction as it has been in
the nets dealt with so far. It is possible for information to flow
from a node back to itself via other nodes. That is, there is feedback
in the network and so they are known as feedback or recurrent
nets as opposed to feedforward nets which were the subject of
the Backpropagation algorithm.
Notice that the flow of
information in this net is not in a single direction as it has been in
the nets dealt with so far. It is possible for information to flow
from a node back to itself via other nodes. That is, there is feedback
in the network and so they are known as feedback or recurrent
nets as opposed to feedforward nets which were the subject of
the Backpropagation algorithm.
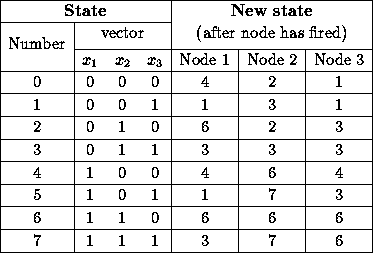
The state of the net at any time is given by the vector of the node
outputs . Suppose we now start this net in some
initial state and choose a node at random and let it update its output
or `fire'. That is, it evaluates its activation in the normal way and
outputs a `1' if this is greater than or equal to zero and a `0'
otherwise. The net now finds itself either in the same state as it
started in, or in a new state which is at Hamming distance one from
the old. We now choose a new node at random to fire and continue in
this way over many steps. What will the behaviour of the net be? For
each state, we may evaluate the next state given each of the three
nodes fires. This gives the following table.
This information may be represented in graphical form as a state transition diagram.
state transition diagram for 3 node net

States are represented by the circles with their associated state number. Directed arcs represent possible transitions between states and the number alongside each arc is the probability that each transition will take place. The states have been arranged in such a way that transitions tend to take place down the diagram; this will be shown to reflect the way the system decreases its energy. The important thing to notice at this stage is that, no matter where we start in the diagram, the net will eventually find itself in one of the states `3' or `6'. These reenter themselves with probability 1. That is they are stable states - once the net finds itself in one of these it stays there. The state vectors for `3' and `6' are (0,1,1) and (1,1,0) respectively and so these are the `memories' stored by the net.