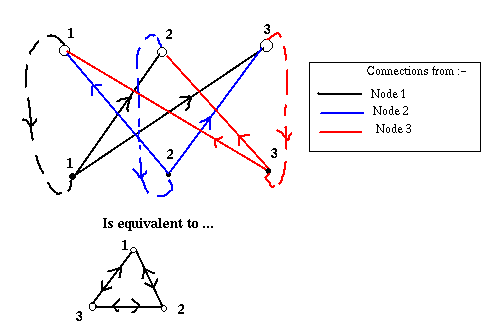
We may draw the connections in, say, a 3 node Hopfield net as follows.
3 node Hopfield net as feedforward with recurrence

Each node may now be thought of as taking part in some input- output
function between the distribution terminals and the node outputs. They
may therefore each be trained with the delta rule. If the
corresponding training set for each one is linearly separable then the
set of stable states may be learnt. However, there is no guarantee now
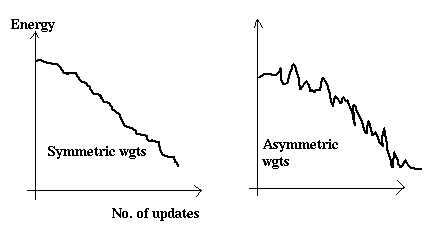
that . The change in energy at each node update is now
no longer necessarily less than or equal to zero. The consequence is
that, given the stable states have been trained, the system moves
through state space with decreasing error towards a stable state but
has, superimposed on this, some noise.
energy v time for symmetric and asymmetric nets